1 量子计算简介
1.1 量子比特与量子纠缠
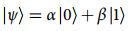 (1)
(1)1.2 量子门
表1 常用量子门 |
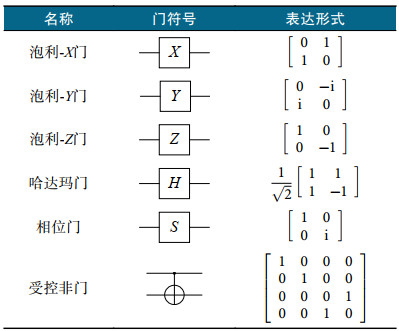 |
1.3 量子计算算法
2 量子计算在轨道交通运输控制的潜在应用
2.1 行车调度组织优化
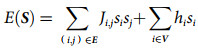 (2)
(2)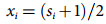 (3)
(3)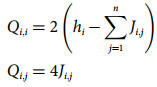 (4)
(4)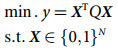 (5)
(5)2.2 列车自动运行控制
2.3 列车群组的动态编解
3 量子计算算法实验分析
3.1 QPSO的仿真实验
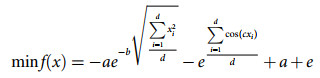 (6)
(6)
|
柴铭,教授,研究方向为轨道交通智能控制与优化,电子信箱:chaiming@bjtu.edu.cn |
收稿日期: 2024-07-23
网络出版日期: 2025-04-11
基金资助
国家自然科学基金项目(52372309)
国家自然科学基金项目(52372310)
国家自然科学基金项目(U2468206)
国家自然科学基金项目(U2468208)
国家自然科学基金项目(U2469211)
国家自然科学基金项目(U22A2046)
国家自然科学基金项目(52172322)
国家自然科学基金项目(52272329)
北京市自然科学基金项目(L231001)
中国国家铁路集团科技研发项目(N2023G058)
版权
Research and application of quantum computing in railway transportation control
Received date: 2024-07-23
Online published: 2025-04-11
Copyright
轨道交通运输规划及控制的数学本质为离散约束下的优化问题,具有NP(non-deterministic polynomial)难的高计算复杂度问题。作为未来计算能力跨越式发展的重要探索方向,量子计算有望为解决现有大规模路网中的复杂问题提供潜在解决方案。介绍了量子计算的基础概念及算法,分析了其在轨道交通领域的潜在应用场景,包括行车调度组织优化、列车自动运行控制和列车群组的动态编解。通过实验验证了量子粒子群算法在解决复杂优化问题中的优势,表明量子计算在处理大规模离散约束优化问题时具有显著的计算效率提升。然而,量子计算技术在轨道交通中的应用仍面临量子比特退相干、硬件集成和结果安全性等挑战。总结了量子计算在轨道交通中的应用前景及可能面临的问题,强调了量子计算技术在推动轨道交通智能化发展中的潜力与挑战。
柴铭 , 梁嘉磊 , 吴博 , 张欣怡 , 谢美玲 . 量子计算在轨道交通运输控制中的研究与应用探索[J]. 科技导报, 2025 , 43(5) : 98 -106 . DOI: 10.3981/j.issn.1000-7857.2024.07.00903
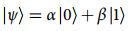 (1)
(1)表1 常用量子门 |
 |
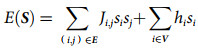 (2)
(2)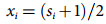 (3)
(3)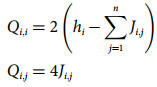 (4)
(4)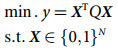 (5)
(5)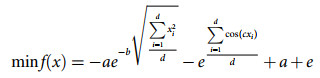 (6)
(6)| 1 |
葛伟涛. 铁路5G网络边缘计算技术研究[J]. 铁路通信信号工程技术, 2023, 20(2): 33-36, 67.
|
| 2 |
韩永建, 李传锋, 郭光灿. 量子计算原理及研究进展[J]. 科技导报, 2017, 35(23): 70- 75.
|
| 3 |
张海懿, 崔潇, 吴冰冰. 量子计算技术产业发展现状与应用分析[J]. 信息通信技术与政策, 2020(7): 20- 26.
|
| 4 |
杨子怡, 文鹏程, 李运喜, 等. 量子计算技术在航空领域的应用分析[J]. 中国新通信, 2023, 25(7): 50- 52.
|
| 5 |
王敬, 李红阳, 赵文玉. 量子计算技术研究及应用探索分析[J]. 信息通信技术与政策, 2022(7): 20- 27.
|
| 6 |
Borowski M, Gora P, Karnas K, et al. New hybrid quantum annealing algorithms for solving vehicle routing problem[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2020: 546-561.
|
| 7 |
Shor P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]//Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, NM, USA: IEEE, 1994: 124-134.
|
| 8 |
Grover L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing-STOC'96. New York: ACM, 1996: 212-219.
|
| 9 |
|
| 10 |
|
| 11 |
Sun J, Feng B, Xu W B. Particle swarm optimization with particles having quantum behavior[C]//Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753). Portland, OR, USA: IEEE, 2004: 325-331.
|
| 12 |
|
| 13 |
阴佳腾. 基于近似动态规划的城轨列车运行一体化调整方法研究[D]. 北京: 北京交通大学, 2018.
|
| 14 |
|
| 15 |
|
| 16 |
陈然一鎏, 赵犇池, 宋旨欣, 等. 混合量子-经典算法: 基础、设计与应用[J]. 物理学报, 2021, 70(21): 36- 51.
|
| 17 |
朱贺田. 货运列车自动驾驶关键技术研究[J]. 铁路通信信号工程技术, 2020, 17(6): 20- 23.
|
| 18 |
唐涛, 罗啸林, 刘宏杰, 等. 城轨列车虚拟编组安全防护与运行控制技术研究进展[J]. 科技导报, 2023, 41(10): 31- 42.
|
| 19 |
|
/
| 〈 |
|
〉 |