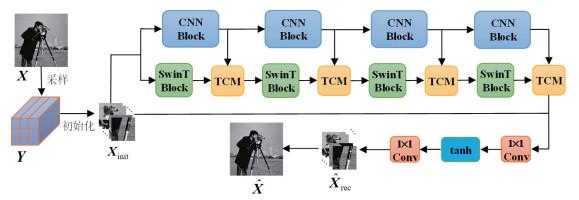
1 并行Transformer和CNN图像压缩感知重构网络
1.1 采样与初始重建子网络
1.2 Transformer-CNN混合重建子网络
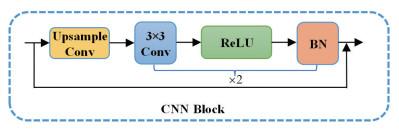
1.2.1 CNN模块
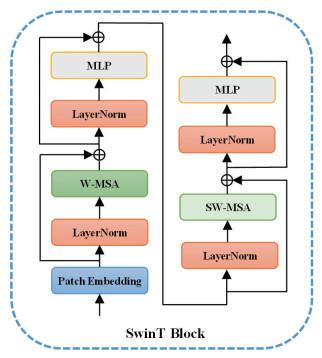
1.2.2 SwinT模块
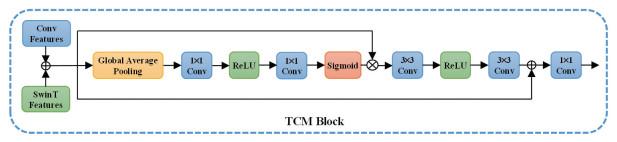
1.2.3 特征融合模块
1.3 损失函数
2 实验结果与分析
2.1 实验设置
2.1.1 数据集和指标
2.1.2 训练详情
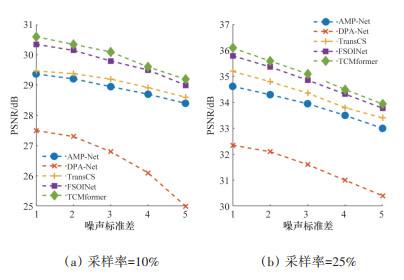
2.2 性能比较
表1 Set11数据集中不同采样率下不同算法重构图像的PSNR(dB)/SSIM对比 |
| 方法 | 10%采样率 | 25%采样率 | 30%采样率 | 40%采样率 | 50%采样率 | 平均 |
| CSNet+ | 28.28/0.8690 | 33.17/0.9420 | 34.36/0.9529 | 36.67/0.9676 | 38.58/0.9763 | 34.21/0.9416 |
| ISTA-Net+ | 26.49/0.8036 | 32.44/0.9237 | 33.70/0.9382 | 36.02/0.9579 | 38.07/0.9706 | 33.34/0.9188 |
| DPA-Net | 27.66/0.8530 | 32.38/0.9311 | 33.35/0.9425 | 35.21/0.9580 | 36.80/0.9685 | 33.08/0.9306 |
| AMP-Net | 29.40/0.8779 | 34.63/0.9481 | 36.03/0.9586 | 38.28/0.9715 | 40.34/0.9804 | 35.74/0.9473 |
| FSOINet | 30.46/0.9023 | 35.80/0.9595 | 37.00/0.9665 | 39.14/0.9764 | 41.08/0.9832 | 36.70/0.9576 |
| CASNet | 30.36/0.9014 | 35.67/0.9591 | 36.92/0.9662 | 39.04/0.9760 | 40.93/0.9826 | 36.58/0.9571 |
| TransCS | 29.54/0.8877 | 35.06/0.9548 | 35.62/0.9588 | 38.46/0.9737 | 40.49/0.9815 | 35.83/0.9513 |
| TCMformer | 30.71/0.9033 | 35.95/0.9602 | 37.15/0.9671 | 39.21/0.9768 | 41.16/0.9838 | 36.84/0.9582 |
表2 Urban100数据集中不同采样率下不同算法重构图像的PSNR(dB)/SSIM对比 |
| 方法 | 10%采样率 | 25%采样率 | 30%采样率 | 40%采样率 | 50%采样率 | 平均 |
| CSNet+ | 24.99/0.7979 | 29.23/0.9070 | 30.35/0.9256 | 32.28/0.9408 | 34.22/0.9588 | 30.21/0.9060 |
| ISTA-Net+ | 23.51/0.7201 | 28.91/0.8834 | 30.15/0.9070 | 32.19/0.9362 | 34.37/0.9571 | 29.83/0.8808 |
| DPA-Net | 24.55/0.7841 | 28.80/0.8944 | 29.47/0.9034 | 31.09/0.9311 | 32.08/0.9447 | 29.20/0.8915 |
| AMP-Net | 26.04/0.8151 | 30.89/0.9202 | 32.19/0.9365 | 34.37/0.9578 | 36.33/0.9712 | 31.96/0.9202 |
| FSOINet | 27.53/0.8627 | 32.62/0.9430 | 33.84/0.9540 | 35.93/0.9688 | 37.80/0.9777 | 33.54/0.9412 |
| CASNet | 27.46/0.8616 | 32.20/0.9396 | 33.37/0.9511 | 35.48/0.9669 | 37.45/0.9777 | 33.19/0.9394 |
| TransCS | 26.72/0.8413 | 31.72/0.9330 | 31.95/0.9483 | 35.22/0.9648 | 37.20/0.9761 | 32.56/0.9327 |
| TCMformer | 27.70/0.8631 | 32.68/0.9445 | 34.10/0.9550 | 36.21/0.9672 | 37.95/0.9788 | 33.73/0.9417 |
3 消融实验与分析
3.1 模块消融
表3 在CS比率为25%时重建Set11数据集图像变体网络的PSNR、SSIM、参数量比较 |
| 方法 | PSNR/dB | SSIM | 参数量/M |
| SwinT/T | 35.82 | 0.9632 | 7.21 |
| w/o TCM Block | 34.63 | 0.9521 | 6.67 |
| SwinT | 35.33 | 0.9528 | 6.98 |
| TCMformer | 35.95 | 0.9602 | 6.85 |
3.2 复杂性分析
表4 在CS比率为50%下重建图像的参数、时间和FLOPs比较 |
| 方法 | 参数量/M | 时间/s | FLOPs/G |
| DPA-Net | 9.78 | 0.0339 | 106.36 |
| AMP-Net | 1.53 | 0.0322 | 23.97 |
| TransCS | 2.28 | 0.4258 | 38.38 |
| TCMformer | 7.31 | 2.4512 | 20.13 |