1 量子计算简介
1.1 量子比特与量子纠缠
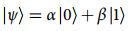 (1)
(1)1.2 量子门
表1 常用量子门 |
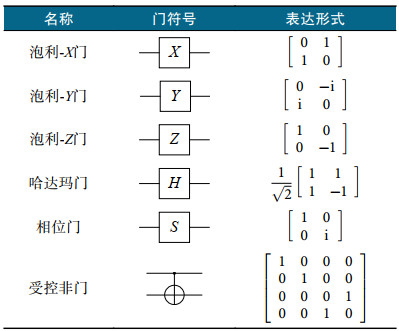 |
1.3 量子计算算法
2 量子计算在轨道交通运输控制的潜在应用
2.1 行车调度组织优化
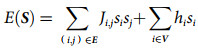 (2)
(2)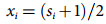 (3)
(3)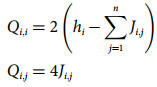 (4)
(4)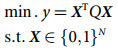 (5)
(5)2.2 列车自动运行控制
2.3 列车群组的动态编解
3 量子计算算法实验分析
3.1 QPSO的仿真实验
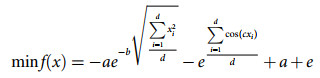 (6)
(6)
Research and application of quantum computing in railway transportation control
Received date: 2024-07-23
Online published: 2025-04-11
Copyright
Ming CHAI , Jialei LIANG , Bo WU , Xinyi ZHANG , Meiling XIE . Research and application of quantum computing in railway transportation control[J]. Science & Technology Review, 2025 , 43(5) : 98 -106 . DOI: 10.3981/j.issn.1000-7857.2024.07.00903
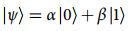 (1)
(1)表1 常用量子门 |
 |
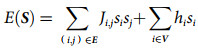 (2)
(2)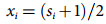 (3)
(3)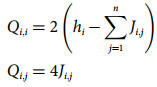 (4)
(4)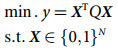 (5)
(5)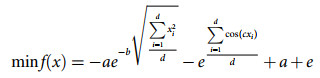 (6)
(6)| 1 |
葛伟涛. 铁路5G网络边缘计算技术研究[J]. 铁路通信信号工程技术, 2023, 20(2): 33-36, 67.
|
| 2 |
韩永建, 李传锋, 郭光灿. 量子计算原理及研究进展[J]. 科技导报, 2017, 35(23): 70- 75.
|
| 3 |
张海懿, 崔潇, 吴冰冰. 量子计算技术产业发展现状与应用分析[J]. 信息通信技术与政策, 2020(7): 20- 26.
|
| 4 |
杨子怡, 文鹏程, 李运喜, 等. 量子计算技术在航空领域的应用分析[J]. 中国新通信, 2023, 25(7): 50- 52.
|
| 5 |
王敬, 李红阳, 赵文玉. 量子计算技术研究及应用探索分析[J]. 信息通信技术与政策, 2022(7): 20- 27.
|
| 6 |
Borowski M, Gora P, Karnas K, et al. New hybrid quantum annealing algorithms for solving vehicle routing problem[M]//Lecture Notes in Computer Science. Cham: Springer International Publishing, 2020: 546-561.
|
| 7 |
Shor P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]//Proceedings 35th Annual Symposium on Foundations of Computer Science. Santa Fe, NM, USA: IEEE, 1994: 124-134.
|
| 8 |
Grover L K. A fast quantum mechanical algorithm for database search[C]//Proceedings of the Twenty-eighth Annual ACM Symposium on Theory of Computing-STOC'96. New York: ACM, 1996: 212-219.
|
| 9 |
|
| 10 |
|
| 11 |
Sun J, Feng B, Xu W B. Particle swarm optimization with particles having quantum behavior[C]//Proceedings of the 2004 Congress on Evolutionary Computation (IEEE Cat. No. 04TH8753). Portland, OR, USA: IEEE, 2004: 325-331.
|
| 12 |
|
| 13 |
阴佳腾. 基于近似动态规划的城轨列车运行一体化调整方法研究[D]. 北京: 北京交通大学, 2018.
|
| 14 |
|
| 15 |
|
| 16 |
陈然一鎏, 赵犇池, 宋旨欣, 等. 混合量子-经典算法: 基础、设计与应用[J]. 物理学报, 2021, 70(21): 36- 51.
|
| 17 |
朱贺田. 货运列车自动驾驶关键技术研究[J]. 铁路通信信号工程技术, 2020, 17(6): 20- 23.
|
| 18 |
唐涛, 罗啸林, 刘宏杰, 等. 城轨列车虚拟编组安全防护与运行控制技术研究进展[J]. 科技导报, 2023, 41(10): 31- 42.
|
| 19 |
|
/
| 〈 |
|
〉 |