1 角谱法卷积误差的产生机制和消除方法
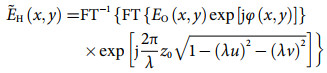 (1)
(1)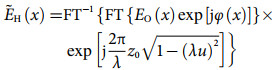 (2)
(2)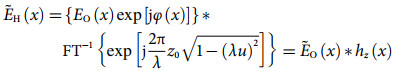 (3)
(3) (4)
(4)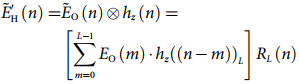 (5)
(5) (6)
(6)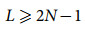 (7)
(7)2 面向相位型全息图的无卷积误差角谱法迭代框架
2.1 基于无卷积误差角谱法的迭代框架
 (8)
(8) (9)
(9)2.2 光学重建结果
3 模型驱动的相位型全息图生成网络
3.1 卷积误差消除的模型驱动相位型全息图生成网络
 (10)
(10)3.2 光学重建结果
4 全息图计算生成方法在三维显示中的应用
4.1 面向三维显示的迭代框架和模型驱动网络
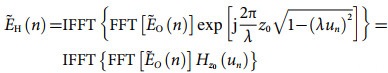 (11)
(11)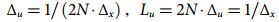 (12)
(12) (13)
(13)
Convolution-error-free model-driven neural network for phase-only computer-generated hologram
Received date: 2024-12-22
Online published: 2025-04-11
Copyright
Zehao HE , Kexuan LIU , Liangcai CAO , Yan ZHANG . Convolution-error-free model-driven neural network for phase-only computer-generated hologram[J]. Science & Technology Review, 2025 , 43(5) : 107 -116 . DOI: 10.3981/j.issn.1000-7857.2024.12.01771
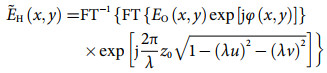 (1)
(1)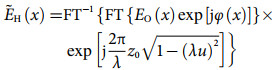 (2)
(2)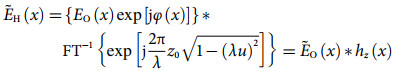 (3)
(3) (4)
(4)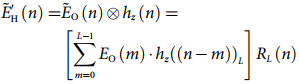 (5)
(5) (6)
(6)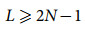 (7)
(7) (8)
(8) (9)
(9) (10)
(10)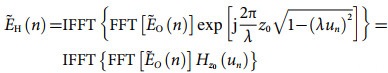 (11)
(11)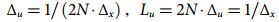 (12)
(12) (13)
(13)| 1 |
曹良才, 何泽浩, 刘珂瑄, 等. 元宇宙中的动态全息三维显示: 发展与挑战(特邀)[J]. 红外与激光工程, 2022, 51(1): 267- 281.
|
| 2 |
何泽浩, 曹良才. 面向沉浸式元宇宙的显示、交互和应用[J]. 科技导报, 2023, 41(5): 6- 14.
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
Shi W, Caballero J, Huszar F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA, 2016: 1874-1883.
|
| 24 |
|
| 25 |
|
/
| 〈 |
|
〉 |